高中數學必修一函數基本特征知識點總結
2018-12-31 19:03:07三好網
1、函數的局部性質——單調性
設函數y=f(x)的定義域為I，如果對應定義域I內的某個區間D內的任意兩個變量x1、x2，當x1< x2時，都有f(x1)<f(x2)，那么y=f(x)在區間D上是增函數，D是函數y=f(x)的單調遞增區間；當x1< x2時，都有f(x1)>f(x2)，那么那么y=f(x)在區間D上是減函數，D是函數y=f(x)的單調遞減區間。
�、藕瘮祬^間單調性的判斷思路
�、≡诮o出區間內任取x1、x2，則x1、x2∈D，且x1< x2。
�、� 做差值f(x1)-f(x2)，并進行變形和配方，變為易于判斷正負的形式。
�、Ｅ袛嘧冃魏蟮谋磉_式f(x1)-f(x2)的符號，指出單調性。
⑵復合函數的單調性
復合函數y=f[g(x)]的單調性與構成它的函數u=g(x)，y=f(u)的單調性密切相關，其規律為“同增異減”；多個函數的復合函數，根據原則“減偶則增，減奇則減”。
⑶注意事項
函數的單調區間只能是其定義域的子區間，不能把單調性相同的區間和在一起寫成并集，如果函數在區間A和B上都遞增，則表示為f(x)的單調遞增區間為A和B，不能表示為A∪B。
2、函數的整體性質——奇偶性
對于函數f(x)定義域內的任意一個x，都有f(x) =f(-x)，則f(x)就為偶函數；
對于函數f(x)定義域內的任意一個x，都有f(x) =-f(x)，則f(x)就為奇函數。
�、牌婧瘮岛团己瘮档男再|
�、o論函數是奇函數還是偶函數，只要函數具有奇偶性，該函數的定義域一定關于原點對稱。
�、⑵婧瘮档膱D像關于原點對稱，偶函數的圖像關于y軸對稱。
⑵函數奇偶性判斷思路
�、∠却_定函數的定義域是否關于原點對稱，若不關于原點對稱，則為非奇非偶函數。
�、⒋_定f(x) 和f(-x)的關系：
若f(x) -f(-x)=0，或f(x) /f(-x)=1，則函數為偶函數；
若f(x)+f(-x)=0，或f(x)/ f(-x)=-1，則函數為奇函數。
3、函數的最值問題
�、艑τ诙魏瘮担门浞椒ǎ瑢⒑瘮祷癁閥=(x-a)2+b的形式，得出函數的最大值或最小值。
⑵對于易于畫出函數圖像的函數，畫出圖像，從圖像中觀察最值。
⑶關于二次函數在閉區間的最值問題
�、∨袛喽魏瘮档捻旤c是否在所求區間內，若在區間內，則接ⅱ，若不在區間內，則接ⅲ。
�、� 若二次函數的頂點在所求區間內，則在二次函數y=ax2+bx+c中，a>0時，頂點為最小值，a<0時頂點為最大值；后判斷區間的兩端點距離頂點的遠近，離頂點遠的端點的函數值，即為a>0時的最大值或a<0時的最小值。
�、� 若二次函數的頂點不在所求區間內，則判斷函數在該區間的單調性
若函數在[a，b]上遞增，則最小值為f(a)，最大值為f(b)；
若函數在[a，b]上遞減，則最小值為f(b)，最大值為f(a)。
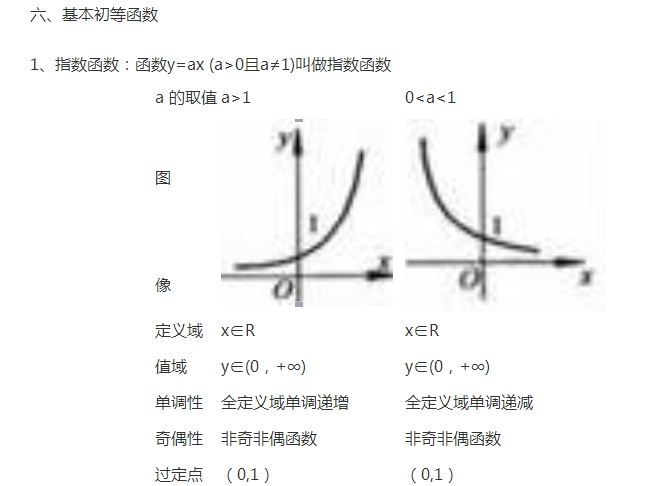
注意：⑴由函數的單調性可以看出，在閉區間[a，b]上，指數函數的最值為：
a>1時，最小值f(a)，最大值f(b)；0<a<1時，最小值f(b)，最大值f(a)。
�、� 對于任意指數函數y=ax (a>0且a≠1)，都有f(1)=a。
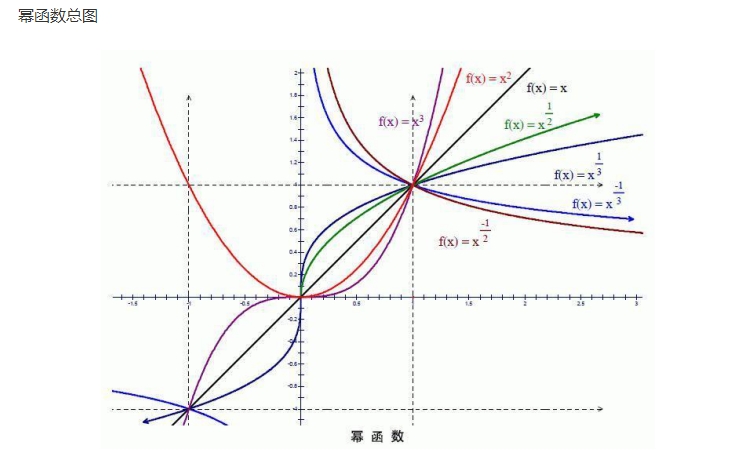
3、冪函數：函數y=xa(a∈R)，高中階段，冪函數只研究第I象限的情況。
�、潘袃绾瘮刀荚�(0，+∞)區間內有定義，而且過定點(1，1)。
�、芶>0時，冪函數圖像過原點，且在(0，+∞)區間為增函數，a越大，圖像坡度越大。
�、莂<0時，冪函數在(0，+∞)區間為減函數。
當x從右側無限接近原點時，圖像無限接近y軸正半軸；
當y無限接近正無窮時，圖像無限接近x軸正半軸。
冪函數總圖見下頁。
4、反函數：將原函數y=f(x)的x和y互換即得其反函數x=f-1(y)。
反函數圖像與原函數圖像關于直線y=x對稱。
